Final Project: Serially looking at your Cereal Choices
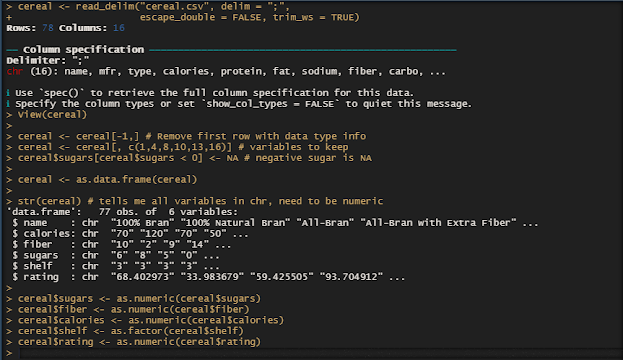
Hi everyone! Almost everyone starts their mornings with a nice bowl of cereal. In the grocery aisle, you choose a box of cheerios and chocolate puffs. However, your decision to buy that cereal may not have been completely your choice at all. You just picked from the options that were conveniently placed in front of you. My project will analyze the relationship between the shelves cereals are placed on to the sugar, fiber, and calories of that cereal. Do the ingredients of cereals, either healthy or sugary, play a role in what shelf cereals are placed on and their ratings? Two Part Analysis Do the ingredients s ugar, calories, and fiber content have a true mean difference with that cereal's placement on shelf 1,2, or 3 (counting from the ground)? I will use boxplots to understand each ingredients distribution in the shelves and perform ANOVA tests to determine if each ingredient is significant for the placement of the the cereal. ANOVA i...





